We use cookies on this website to distinguish you from other users. We use this data to improve our content experience and for targeted advertising. By continuing to use this website you consent to our use of cookies. For more information, please see our Cookie Policy.

spafe.utils.converters#

Description : Frequency converters implementation.
Copyright (c) 2019-2024 Ayoub Malek. This source code is licensed under the terms of the BSD 3-Clause License. For a copy, see <https://github.com/SuperKogito/spafe/blob/master/LICENSE>.

spafe.utils.converters.hz2erb(f: float, approach: typing_extensions.Literal[Glasberg] = 'Glasberg') → float[source]#

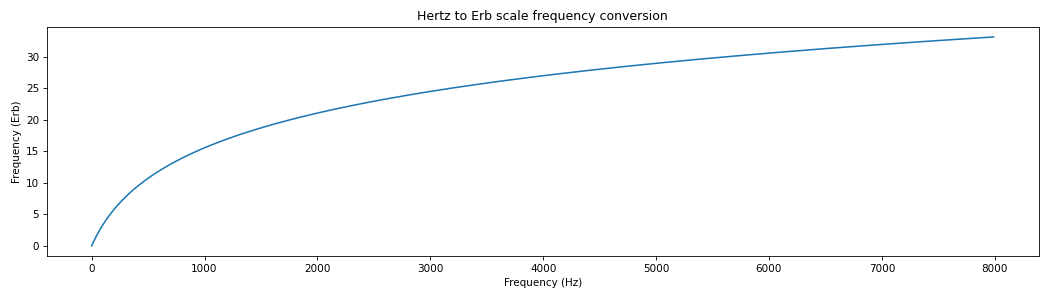
Convert Hz frequencies to Erb as referenced in [Glasberg].

Parameters

f (float) – input frequency [Hz].
approach (str) – conversion approach. (Default is “Glasberg”).

Returns

frequency in Erb [Erb].

Return type

(float)

Note

Glasberg (1990) :

\(fe = A . log_{10}(1 + f . 0.00437)\)
\(f = \frac{10^{\frac{fe}{A}} - 1}{0.00437}\)

where \(A = \frac{1000 . log_{e}(10)}{24.7 . 4.37}\)

! might raise: RuntimeWarning: invalid value encountered in log10

References

Glasberg(1,2): : Glasberg B. R., and Moore B. C. J. “Derivation of Auditory Filter Shapes from Notched-Noise Data.” Hearing Research. Vol. 47, Issues 1–2, 1990, pp. 103–138.

Examples

import matplotlib.pyplot as plt
from spafe.utils.converters import hz2erb

# generate freqs array -> convert freqs
hz_freqs = [freq for freq in range(0, 8000, 10)]
erb_freqs = [hz2erb(freq) for freq in hz_freqs]

# visualize conversion
plt.figure(figsize=(14,4))
plt.plot(hz_freqs, erb_freqs)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Frequency (Erb)")
plt.title("Hertz to Erb scale frequency conversion")
plt.tight_layout()
plt.show()

spafe.utils.converters.erb2hz(fe: float, approach: typing_extensions.Literal[Glasberg] = 'Glasberg') → float[source]#

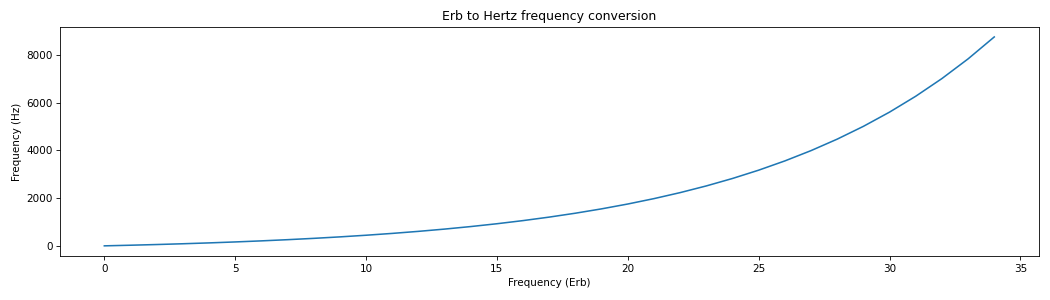
Convert Erb frequencies to Hz as referenced in [Glasberg].

Parameters

fe (float) – input frequency [Erb].
approach (str) – conversion approach. (Default is “Glasberg”).

Returns

frequency in Hz [Hz].

Return type

(float)

Note

Glasberg (1990) :

\(fe = A . log_{10}(1 + f . 0.00437)\)
\(f = \frac{10^{\frac{fe}{A}} - 1}{0.00437}\)

where \(A = \frac{1000 . log_{e}(10)}{24.7 . 4.37}\)

! might raise: RuntimeWarning: invalid value encountered in log10

Examples

import matplotlib.pyplot as plt
from spafe.utils.converters import erb2hz

# generate freqs array -> convert freqs
erb_freqs = [freq for freq in range(0, 35, 1)]
hz_freqs = [erb2hz(freq) for freq in erb_freqs]

# visualize conversion
plt.figure(figsize=(14,4))
plt.plot(erb_freqs, hz_freqs)
plt.xlabel("Frequency (Erb)")
plt.ylabel("Frequency (Hz)")
plt.title("Erb to Hertz frequency conversion")
plt.tight_layout()
plt.show()

spafe.utils.converters.hz2bark(f: float, approach: typing_extensions.Literal[Wang, Tjomov, Schroeder, Terhardt, Zwicker, Traunmueller] = 'Wang') → float[source]#

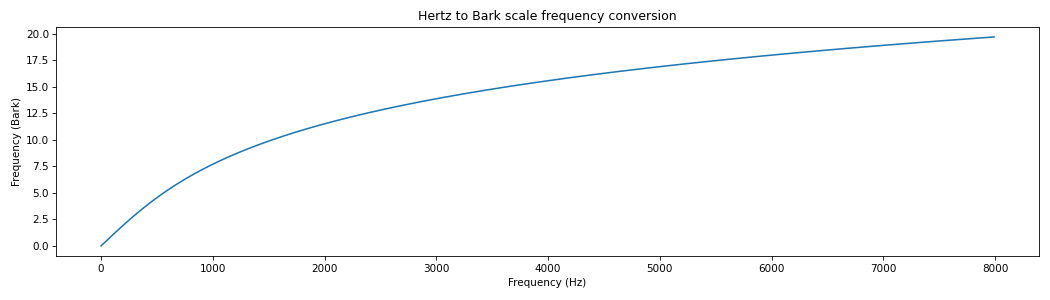
Convert Hz frequencies to Bark as mentioned in [Carter] and [Traunmueller].

Parameters

f (float) – input frequency [Hz].
approach (str) – conversion approach. (Default is “Wang”).

Returns

frequency in Bark [Bark].

Return type

(float)

Note

Tjomov (1971) :

\(fb = 6.7 . sinh^{-1}(\frac{f+20}{600})\)
\(f = 600 . sinh(\frac{fb}{6.7}) - 20\)

Schroeder (1977) :

\(fb = 7 . sinh^{-1}(\frac{f}{650})\)
\(f = 650 . sinh(\frac{fb}{7})\)

Terhardt (1979) :

\(fb = 13.3*tan^{-1}(\frac{0.75 . f}{1000})\)
\(f = (1000/0.75)*tan(\frac{fb}{13})\)

Zwicker & Terhardt (1980) :

\(fb = 8.7 + 14.2 . log10(\frac{f}{1000})\)
\(f = 10^{(\frac{fb-8.7}{14.2} + 3)}\)

Traunmueller (1983) :

\(fb = (\frac{26.81*f}{1+1960}) - 0.53\)
\(f = 1960 . (\frac{fb+0.53}{26.28-fb})\)

Wang, Sekey & Gersho (1992) :

\(fb = 6 . sinh^{-1}(\frac{f}{600})\)
\(f = 600 . sinh(\frac{fb}{6})\)

Examples

import matplotlib.pyplot as plt
from spafe.utils.converters import hz2bark

# generate freqs array -> convert freqs
hz_freqs = [freq for freq in range(0, 8000, 10)]
bark_freqs = [hz2bark(freq) for freq in hz_freqs]

# visualize conversion
plt.figure(figsize=(14,4))
plt.plot(hz_freqs, bark_freqs)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Frequency (Bark)")
plt.title("Hertz to Bark scale frequency conversion")
plt.tight_layout()
plt.show()

spafe.utils.converters.bark2hz(fb: float, approach: typing_extensions.Literal[Wang, Tjomov, Schroeder, Terhardt, Zwicker, Traunmueller] = 'Wang') → float[source]#

Convert Bark frequencies to Hz as mentioned in [Carter] and [Traunmueller].

Parameters

fb (float) – input frequency [Bark].
approach (str) – conversion approach. (Default is “Wang”).

Returns

frequency in Hz [Hz].

Return type

(float)

Note

Tjomov (1971) :

\(fb = 6.7 . sinh^{-1}(\frac{f+20}{600})\)
\(f = 600 . sinh(\frac{fb}{6.7}) - 20\)

Schroeder (1977) :

\(fb = 7 . sinh^{-1}(\frac{f}{650})\)
\(f = 650 . sinh(\frac{fb}{7})\)

Terhardt (1979) :

\(fb = 13.3*tan^{-1}(\frac{0.75 . f}{1000})\)
\(f = (1000/0.75)*tan(\frac{fb}{13})\)

Zwicker & Terhardt (1980) :

\(fb = 8.7 + 14.2 . log10(\frac{f}{1000})\)
\(f = 10^{(\frac{fb-8.7}{14.2} + 3)}\)

! might raise RuntimeWarning: divide by zero encountered in log10

Traunmueller (1983) :

\(fb = (\frac{26.81*f}{1+1960}) - 0.53\)
\(f = 1960 . (\frac{fb+0.53}{26.28-fb})\)

Wang, Sekey & Gersho (1992) :

\(fb = 6 . sinh^{-1}(\frac{f}{600})\)
\(f = 600 . sinh(\frac{fb}{6})\)

References

Carter(1,2): Carter, P., “Sonification seminar – 10/9/03”, CCRMA.Stanford.edu., https://ccrma.stanford.edu/courses/120-fall-2003/lecture-5.html
Traunmueller(1,2): Traunmueller, H. (1990). Analytical expressions for the tonotopic sensory scale. The Journal of the Acoustical Society of America, 88(1), 97–100. doi:10.1121/1.399849

Examples

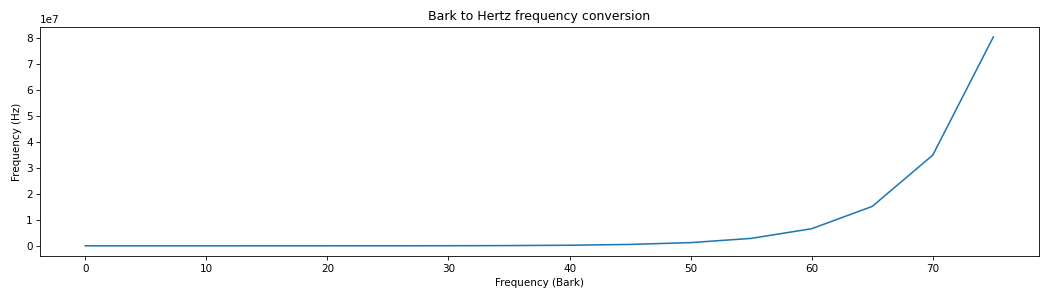
import matplotlib.pyplot as plt
from spafe.utils.converters import bark2hz

# generate freqs array -> convert freqs
bark_freqs = [freq for freq in range(0, 80, 5)]
hz_freqs = [bark2hz(freq) for freq in bark_freqs]

# visualize conversion
plt.figure(figsize=(14,4))
plt.plot(bark_freqs, hz_freqs)
plt.xlabel("Frequency (Bark)")
plt.ylabel("Frequency (Hz)")
plt.title("Bark to Hertz frequency conversion")
plt.tight_layout()
plt.show()

spafe.utils.converters.hz2mel(f: float, approach: typing_extensions.Literal[Oshaghnessy, Lindsay] = 'Oshaghnessy') → float[source]#

Convert a value in Hertz to Mels [Oshaghnessy], [Beranek] and [Lindsay].

Parameters

f (float) – input frequency [Hz].
approach (str) – conversion approach. (Default is “Oshaghnessy”).

Returns

frequency in Mel scale [Mel].

Return type

(float)

Note

Oshaghnessy (1987) :

\(fm = 2595 . log_{10}(1 + \frac{f}{700})\)
\(f = 700 . (10^{(\frac{fm}{2595} - 1)}\)

Beranek (1987) :

\(fm = 1127 . log_{e}(1 + \frac{f}{700})\)
\(f = 700 . exp(\frac{fm}{1127} - 1)\)

Both previous equations correspond to each other.

Lindsay (1977) :

\(fm = 2410 . log_{10}(1 + \frac{f}{625})\)
\(f = 625 . (10^{(\frac{fm}{2410} - 1)}\)

References

Oshaghnessy: : O’Shaghnessy, Douglas. Speech Communication: Human and Machine. Reading, MA: Addison-Wesley Publishing Company, 1987.
Beranek: : Beranek L.L. Acoustic Measurements, (1949) New York: Wiley.
Lindsay: : Lindsay, Peter H.; & Norman, Donald A. (1977). Human information processing: An introduction to psychology (2nd ed.). New York: Academic Press.

Examples

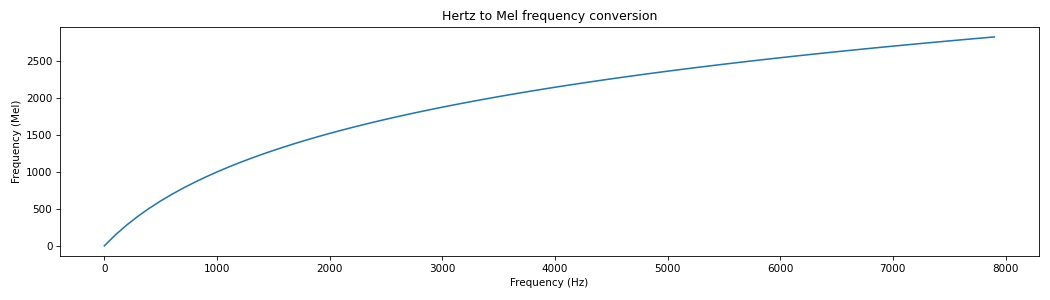
import matplotlib.pyplot as plt
from spafe.utils.converters import hz2mel

# generate freqs array -> convert freqs
hz_freqs = [freq for freq in range(0, 8000, 100)]
mel_freqs = [hz2mel(freq) for freq in hz_freqs]

# visualize conversion
plt.figure(figsize=(14,4))
plt.plot(hz_freqs, mel_freqs)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Frequency (Mel)")
plt.title("Hertz to Mel frequency conversion")
plt.tight_layout()
plt.show()

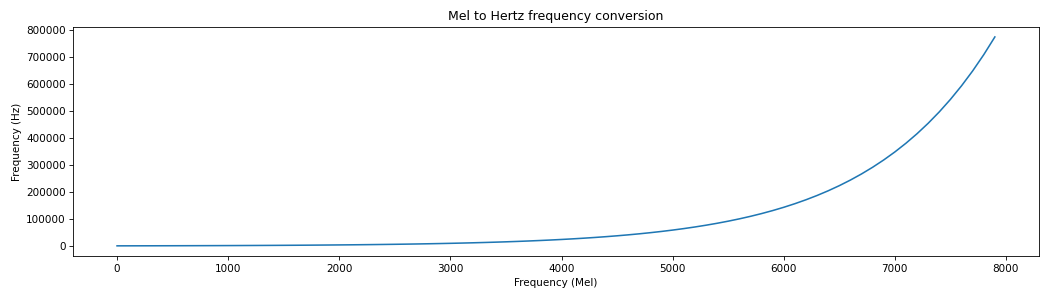
spafe.utils.converters.mel2hz(fm: float, approach: typing_extensions.Literal[Oshaghnessy, Lindsay] = 'Oshaghnessy') → float[source]#

Convert a value in Mels to Hertz

Parameters

fm (float) – input frequency [Mel].
approach (str) – conversion approach. (Default is “Wang”).

Returns

frequency in Hz [Hz].

Return type

(float)

Examples

import matplotlib.pyplot as plt
from spafe.utils.converters import mel2hz

# generate freqs array -> convert freqs
mel_freqs = [freq for freq in range(0, 8000, 100)]
hz_freqs = [mel2hz(freq) for freq in mel_freqs]

# visualize conversion
plt.figure(figsize=(14,4))
plt.plot(mel_freqs, hz_freqs)
plt.xlabel("Frequency (Mel)")
plt.ylabel("Frequency (Hz)")
plt.title("Mel to Hertz frequency conversion")
plt.tight_layout()
plt.show()

spafe.utils.cepstral

spafe.utils.filters